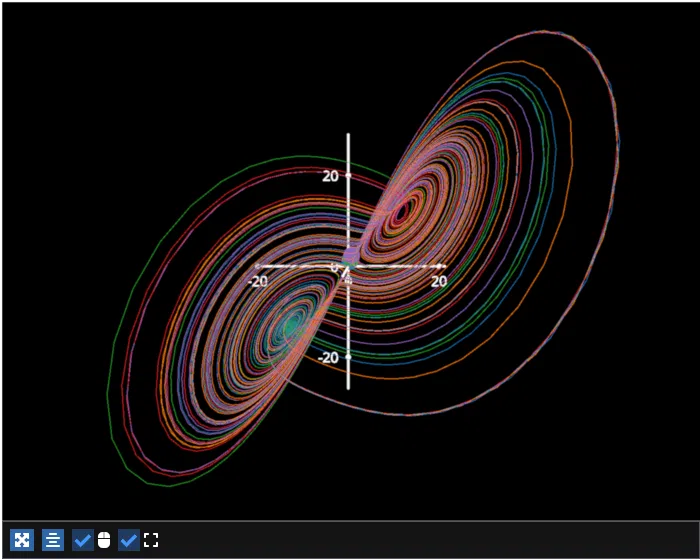
Lorenz System Animation

Example of the Lorenz attractor.

/opt/hostedtoolcache/Python/3.12.7/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:266: RuntimeWarning: divide by zero encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.7/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:266: RuntimeWarning: invalid value encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.7/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:278: RuntimeWarning: invalid value encountered in divide
  screen_sel = (ndc_sel[:, :2] / ndc_sel[:, 3:4]) * half_canvas_size
/home/runner/work/fastplotlib/fastplotlib/fastplotlib/graphics/_features/_base.py:18: UserWarning: casting float64 array to float32
  warn(f"casting {array.dtype} array to float32")

# test_example = false

import fastplotlib as fpl
import numpy as np


# generate data
def lorenz(xyz, *, s=10, r=28, b=2.667):
    """
    Parameters
    ----------
    xyz : array-like, shape (3,)
       Point of interest in three-dimensional space.
    s, r, b : float
       Parameters defining the Lorenz attractor.

    Returns
    -------
    xyz_dot : array, shape (3,)
       Values of the Lorenz attractor's partial derivatives at *xyz*.
    """
    x, y, z = xyz
    x_dot = s * (y - x)
    y_dot = r * x - y - x * z
    z_dot = x * y - b * z
    return np.array([x_dot, y_dot, z_dot])


dt = 0.01
num_steps = 3_000

lorenz_data = np.empty((5, num_steps + 1, 3))

for i in range(5):
    xyzs = np.empty((num_steps + 1, 3))  # Need one more for the initial values
    xyzs[0] = (0., (i * 0.3) + 1, 1.05)  # Set initial values
    # Step through "time", calculating the partial derivatives at the current point
    # and using them to estimate the next point
    for j in range(num_steps):
        xyzs[j + 1] = xyzs[j] + lorenz(xyzs[j]) * dt

    lorenz_data[i] = xyzs

figure = fpl.Figure(
    cameras="3d",
    controller_types="fly",
    size=(700, 560)
)

lorenz_line = figure[0, 0].add_line_collection(data=lorenz_data, thickness=.1, cmap="tab10")

scatter_markers = list()

for graphic in lorenz_line:
    marker = figure[0, 0].add_scatter(graphic.data.value[0], sizes=16, colors=graphic.colors[0])
    scatter_markers.append(marker)

# initialize time
time = 0


def animate(subplot):
    global time

    time += 2

    if time >= xyzs.shape[0]:
        time = 0

    for scatter, g in zip(scatter_markers, lorenz_line):
        scatter.data = g.data.value[time]


figure[0, 0].add_animations(animate)

figure.show()

# set initial camera position to make animation in gallery render better
figure[0, 0].camera.world.z = 80

# NOTE: `if __name__ == "__main__"` is NOT how to use fastplotlib interactively
# please see our docs for using fastplotlib interactively in ipython and jupyter
if __name__ == "__main__":
    print(__doc__)
    fpl.run()