Swirling vectors

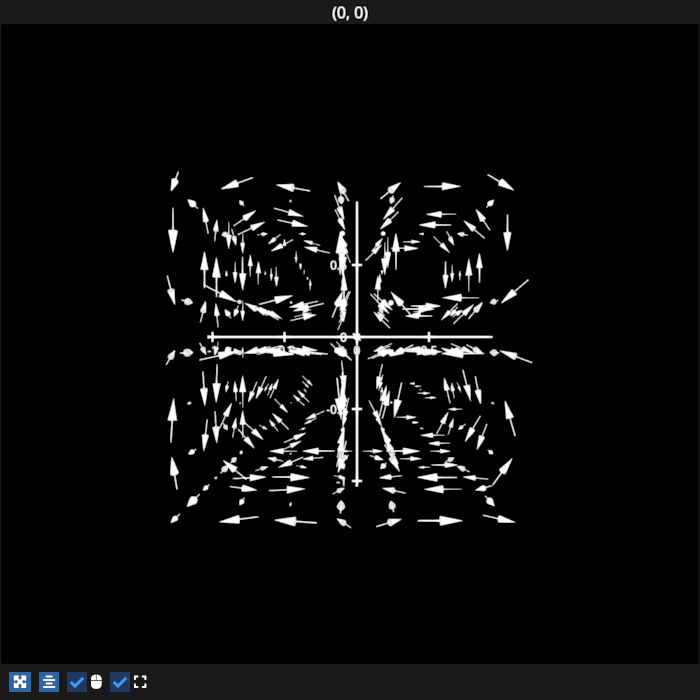
Example showing swirling vectors. Similar to matplotlib quiver.

/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:400: RuntimeWarning: divide by zero encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:400: RuntimeWarning: invalid value encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:412: RuntimeWarning: invalid value encountered in divide
  screen_sel = (ndc_sel[:, :2] / ndc_sel[:, 3:4]) * half_canvas_size

# test_example = true

import numpy as np
import fastplotlib as fpl

figure = fpl.Figure(cameras="3d", controller_types="orbit", size=(700, 700))

start, stop, step = -1, 1, 0.3

# Make the grid
x, y, z = np.meshgrid(
    np.arange(start, stop, step),
    np.arange(start, stop, step),
    np.arange(start, stop, step),
)

# Make the direction data for the arrows
u = np.sin(np.pi * x) * np.cos(np.pi * y) * np.cos(np.pi * z)
v = -np.cos(np.pi * x) * np.sin(np.pi * y) * np.cos(np.pi * z)
w = np.sqrt(2.0 / 3.0) * np.cos(np.pi * x) * np.cos(np.pi * y) * np.sin(np.pi * z)

positions = np.column_stack([x.ravel(), y.ravel(), z.ravel()])
directions = np.column_stack([u.ravel(), v.ravel(), w.ravel()])


vectors = figure[0, 0].add_vectors(
    positions=positions,
    directions=directions,
)

figure.show()


# NOTE: fpl.loop.run() should not be used for interactive sessions
# See the "JupyterLab and IPython" section in the user guide
if __name__ == "__main__":
    print(__doc__)
    fpl.loop.run()