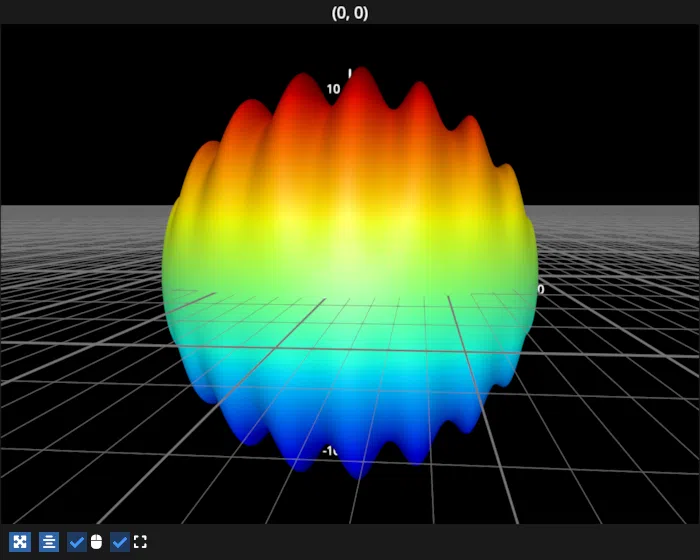
Sphere ripple animation

Example of a sphere with a ripple effect by setting the data on every render.

/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:400: RuntimeWarning: divide by zero encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:400: RuntimeWarning: invalid value encountered in divide
  screen_full = (ndc_full[:, :2] / ndc_full[:, 3:4]) * half_canvas_size
/opt/hostedtoolcache/Python/3.12.12/x64/lib/python3.12/site-packages/pygfx/objects/_ruler.py:412: RuntimeWarning: invalid value encountered in divide
  screen_sel = (ndc_sel[:, :2] / ndc_sel[:, 3:4]) * half_canvas_size

# test_example = false

import fastplotlib as fpl
import numpy as np

figure = fpl.Figure(size=(700, 560), cameras="3d", controller_types="orbit")

# create an ellipsoid from spherical coordinates
# see this for reference: https://mathworld.wolfram.com/SphericalCoordinates.html
# phi and theta are swapped in this example w.r.t. the wolfram alpha description
radius = 10
nx = 250
phi = np.linspace(0, np.pi * 2, num=nx, dtype=np.float32)
ny = 250
theta = np.linspace(0, np.pi, num=ny, dtype=np.float32)

phi_grid, theta_grid = np.meshgrid(phi, theta)

# convert to cartesian coordinates
theta_grid_sin = np.sin(theta_grid)
x = radius * np.cos(phi_grid) * theta_grid_sin * -1
y = radius * np.cos(theta_grid)

ripple_amplitude = 1.0
ripple_frequency = 20.0
ripple = ripple_amplitude * np.sin(ripple_frequency * theta_grid)

z_ref = radius * np.sin(phi_grid) * theta_grid_sin
z = z_ref * (1 + ripple / radius)

sphere = figure[0, 0].add_surface(
    np.dstack([x, y, z]),
    mode="phong",
    colors="red",
    cmap="jet",
)

# display xz plane as a grid
figure[0, 0].axes.grids.xy.visible = True
figure.show()

figure[0, 0].camera.show_object(sphere.world_object, (10, 1, -1), up=(0, 0, 1))
figure[0, 0].camera.zoom = 1.3


start = 0


def animate():
    global start
    theta = np.linspace(start, start + np.pi, num=ny, dtype=np.float32)
    _, theta_grid = np.meshgrid(phi, theta)
    ripple = ripple_amplitude * np.sin(ripple_frequency * theta_grid)

    z = z_ref * (1 + ripple / radius)

    sphere.data = np.dstack([x, y, z])

    start += 0.005

    if start > np.pi * 2:
        start = 0


figure[0, 0].add_animations(animate)


# NOTE: fpl.loop.run() should not be used for interactive sessions
# See the "JupyterLab and IPython" section in the user guide
if __name__ == "__main__":
    print(__doc__)
    fpl.loop.run()